 5.0 WAVES
5.0 WAVES A wave is a disturbance in a medium that carries energy without a net movement of particles. It may take the form of elastic deformation, a variation of pressure, electric or magnetic intensity, electric potential, or temperature.
5.1 INTRODUCTION OF WAVES ⇒ Transfers energy.
⇒ Usually involves a periodic, repetitive Movement.
⇒ Does not result in a net movement of the medium or particles in the medium (mechanical wave).
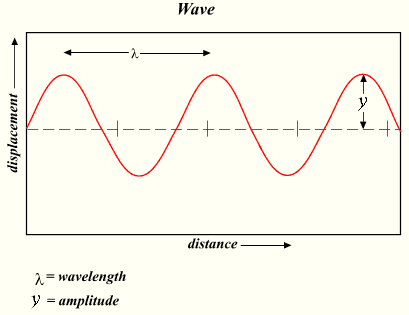
There are some basic descriptors of a wave. Wavelength is the distance between an identical part of the wave. Amplitude is maximum displacement from the neutral position. This represents the energy of the wave. Greater amplitude carries greater energy. Displacement is the position of a particular point in the medium as it moves as the wave passes. Maximum displacement is the amplitude of the wave
Frequency
(ƒ) is the number of repetitions per second in
Hz, s -1 Period
(T) is the time for one wavelength to pass a point. T =
ƒ-1 The velocity (v) of the wave is the speed that a specific part of the wave passes a point. The speed of a light wave is c.
5.2 TYPES OF WAVES A wave can be transverse or longitudinal depending on the direction of its oscillation. Transverse waves occur when a disturbance causes oscillations perpendicular (at right angles) to the propagation (the direction of energy transfer). Longitudinal waves occur when the oscillations are parallel to the direction of propagation. While mechanical waves can be both transverse and longitudinal, all electromagnetic waves are transverse. Sound, for example, is a longitudinal wave.
1. Transverse Waves : Transverse waves propagate through media with a speed orthogonally to the direction of energy transfer. Transverse waves oscillate in the z-y plane but travel along the x axis. A transverse wave has a speed of propagation given by the equation
v = fλ. The direction of energy transfer is perpendicular to the motion of the wave.
Examples of transverse waves: ⇒ Water waves (ripples of gravity waves, not sound through water)
⇒ Light waves
⇒ S-wave earthquake waves
⇒ Stringed instruments
⇒ Torsion wave
When a wave travels through a medium–i.e., air, water, etc., or the standard reference medium (vacuum)–it does so at a given speed: this is called the speed of propagation. The speed at which the wave propagates is denoted and can be found using the following formula:
v = fλ where v is the speed of the wave, f is the frequency , and is the wavelength. The wavelength spans crest to crest while the amplitude is 1/2 the total distance from crest to trough. Transverse waves have their applications in many areas of physics.
2. Longitudinal Waves : A longitudinal wave has the movement of the particles in the medium in the same dimension as the direction of movement of the wave. Longitudinal waves, sometimes called compression waves, oscillate in the direction of propagation. While longitudinal waves oscillate in the direction of propagation, they do not displace mass since the oscillations are small and involve an equilibrium position.
Longitudinal waves have the same direction of vibration as their direction of travel. This means that the movement of the medium is in the same direction as the motion of the wave. Some longitudinal waves are also called compressional waves or compression waves. An easy experiment for observing longitudinal waves involves taking a Slinky and holding both ends. After compressing and releasing one end of the Slinky (while still holding onto the end), a pulse of more concentrated coils will travel to the end of the Slinky.
Like transverse waves, longitudinal waves do not displace mass. The difference is that each particle which makes up the medium through which a longitudinal wave propagates oscillates along the axis of propagation. In the example of the Slinky, each coil will oscillate at a point but will not travel the length of the Slinky. It is important to remember that energy, in this case in the form of a pulse, is being transmitted and not the displaced mass.
Longitudinal waves can sometimes also be conceptualized as pressure waves. The most common pressure wave is the sound wave. Sound waves are created by the compression of a medium, usually air.
Longitudinal sound waves are waves of alternating pressure deviations from the equilibrium pressure, causing local regions of compression and rarefaction. Matter in the medium is periodically displaced by a sound wave, and thus oscillates.
When people make a sound, whether it is through speaking or hitting something, they are compressing the air particles to some significant amount. By doing so, they create transverse waves. When people hear sounds, their ears are sensitive to the pressure differences and interpret the waves as different tones.
Examples of longitudinal waves: ⇒ Sound waves
⇒ P-type earthquake waves
⇒ Compression wave
Parts of longitudinal waves: ⇒ Compression: where the particles are close together.
⇒ Rarefaction: where the particles are spread apart.
5.3 CLASS OF WAVES 1. Electromagnetic Waves: These waves are the disturbance that does not need any object medium for propagation and can easily travel through the vacuum. They are produced due to various magnetic and electric fields. The periodic changes that take place in magnetic electric fields and therefore known as Electromagnetic Wave
 Electromagnetic Wave
Electromagnetic Wave A wave which needs a medium in order to propagate itself. Sound waves, waves in a Slinky, and water waves are all examples of this.
i. Water Waves: The particles which make up a water wave move in circular paths. If the waves move slower than the wind above them, energy is transfered from the wind to the waves. The oscillations are greatest on the surface of the wave and become weaker deeper in the fluid.
Water waves, which can be commonly observed in our daily lives, are of specific interest to physicists. Describing detailed fluid dynamics in water waves is beyond the scope of introductory physics courses. Although we often observe water wave propagating in 2D, in this atom we will limit our discussion to 1D propagation.
 Water waves
Water waves It is the total distance covered by the wave in a given time period. The formula for wave speed is given as,
Wave Speed = Distance Covered/Time taken5.5 TERMS USED IN WAVE MOTION The prime properties of waves are as follows: i. Amplitude – Wave is an energy transport phenomenon. Amplitude is the height of the wave, usually measured in meters. Amplitude is directly related to the amount of energy carried by a wave.
ii. Wavelength – The distance between identical points in the adjacent cycles or crests of a wave is called wavelength. It is also measured in meters.
iii. Period – The period of a wave is the time for a particle on a medium to make one complete vibrational cycle. As the period is a time, hence is measured in units of time such as seconds or minutes.
iv. Frequency – Frequency of a wave is the number of waves passing a point in a certain time. The unit of frequency is hertz (Hz) which is equal to one wave per second.
v. Phase – is define as the ratio of the displacement of the vibrating particles at any instant to the amplitude of the vibrating particles
The period is the reciprocal of the frequency and vice versa.
Period = 1/Frequency
OR
Frequency = 1/Period vi. Speed – The speed of an object means how fast an object moves and is usually expressed as the distance traveled per time of travel. The speed of a wave refers to the distance traveled by a given point on the wave (crest) in a given interval of time. That is –
Speed = Distance/Time Speed of a wave is thus measured in meter/second i.e. m/s.5.6 PROPERTIES OF WAVES I. Reflection: This is the change in the direction of waves when they hit an obstacle. The type of waves formed depends on the type of obstacle they hit or meet. For instance, straight and parallel waves are set up from a plane metal strip standing upright in the water of a ripple tank. Similarly, when the plane metal is replaced by curved metal strips, the reflection rays form a spherical waves.
II. Refraction: This occurs between two media when wave direction of propagation changes as it enters a different medium. When straight waves pass from deep to shallow water, their wavelength becomes shorter, During this process, the frequency remains the same but the wavelength varies.
III. Diffraction: This occurs when waves bend round obstacles. it is also the spreading of waves after passing through tiny opening, aperture, a hole or a slit. The smaller the width of the aperture, the smaller the wavelength, the greater will be spreading of the waves. Similarly, the bigger the width of the aperture, the longer the wavelength, the smaller will be spreading of the waves.
IV. Interference: This occurs when two waves from a source cross each others path. if the crest of one arrives simultaneously as the thoughts of the other, it is referred to as constructive interference. But if the crest of one does not arrives simultaneously as the thought of others, it is referred as destructive interference.
V. Polarization: It simply means that confinement of waves in one direction occurs only in transverse waves. Plane polarization of light means the fluctuation are constructed to vibrate only in one plane perpendicular to the direction of the light.
5.7 WORKED EXAMPLE EXAMPLE 1:
A source of sound produce waves in air of wavelength 3.42m. If the speed in air is 330m/s, What is the period of vibration.
Solution; v = 330m/s , λ = 3.42m , T = ?
V = λ/T
T = λ/V
T = 3.42/330
T = 1.036 x 10
-3 EXAMPLE 2: A Wave has frequency of 30Hz and wavelength of 40cm. What is the velocity of the wave ?
Solution; V = λ/T
V = 30 x 0.4
V = 12m/s
N.B A Progressive wave can be represented by the equation,
y = A sin (ωt - φ) where; y = Vertical displacement
x = Horizontal displacement
A = Amplitude
ω = Angular velocity
φ = Phase angle
ω = 2πf = 2πV/λ = 2π/T
K = 2π/λ , φ = Kx = 2πx/λ
y = A sin (ωt - Kx) ------- (i)
y = A sin 2πft - 2πx/λ
= A sin 2π ft - x/λ --------(ii)
y = A sin 2πvt/λ - 2πx/λ
= A sin 2π/λ (vt - x) -------(iii)
y = A sin 2πt/T - 2πx/λ
= A sin 2π t/T - x/λ ---------(iv)
EXAMPLE 3: The plane progressive wave is represented by the equation
y = 4 sin (100πt - 50πx) Find the (i)amplitude (ii)frequency (iii)wavelength (iv)velocity
Solution; FORMULA is y = A sin (2πft - 2π/λ)x from y = 4 sin (100πt - 50πx)
(i) amplitude = 4m (i.e A)
(ii) Frequency =
2πft = 100πt
f = 100πt/2πt
f= 50Hz
(iii) Wavelength =
2π/λ = 50π
λ= 2π/50π
λ = 0.04m i.e 4cm
(v) Velocity =
v = fλ
v = 50 x 0.04
v = 2m/s
[1] What is Electromagnetic waves
[2] Give 3 example of electromagnetic waves
[3] Explain the following ("Frequency, Amplitude, Wavelength")
[4] Calculate the period of a wave of wavelength 0.6m and speed 300m/s
[5] Name the two classes of waves and explain them
[6] State the properties of waves
[7] Explain the following (i)Interference (ii)Diffraction
[8] A progressive wave is given y = 0.5 sin 2π(40t - 20x). Find (i)wavelength
[9] Differentiate between interference and polarization as applied to waves
[10] Mention 2 uses of Polaroids.





